Download this notebook

Status: Draft

Rao Blackwellization for Variance Reduction

import numpy as np

import matplotlib.pyplot as plt
%matplotlib inline

If we have a function$ J(X,Y) $ of two random variables$ X $ and$ Y $ and we want to compute the expectation$ \bar J = \mathbb E_{X,Y}[J(X,Y)] $.

We define $ \bar J(X)= \mathbb E_{Y}[J(X,Y)\mid X] = \int_\mathcal{Y} J(X,Y) p( y \mid X) dy $

Note that: $ \int_\mathcal{X} \int_\mathcal{Y} p(x, y) J(X=x,Y=y) p(x, y) dx dy= \int_\mathcal{X} p(x) \left( \int_\mathcal{Y} J(X=x, Y=y) p( y \mid X=x) dy \right) dx $ i.e.

$ \mathbb E_{X,Y}[J(X,Y)] = \mathbb E_{X} [\bar J(X)] $

So, we can use$ \bar J(X) $ instead of$ J(X, Y) $ in a Monte-Carlo estimate, e.g. if we can compute$ \bar J(X) $ analytically.

Variance of$ J(X,Y) $ vs$ \bar J(X) $

by the "law of total variance" we have

$ \begin{align} var(J(X,Y)) &= \mathbb E\left[ var(J(X,Y) \mid X) \right] + var( \mathbb E\left[ J(X,Y) \mid X \right] )\\ &= \mathbb E\left[ \mathbb E[(J(X,Y)-\bar J(X))^2\mid X]- (\mathbb E[J(X,Y)-\bar J(X)\mid X])^2 \right] + var( \bar J(X) )\\ &= \mathbb E\left[ \mathbb E[(J(X,Y)-\bar J(X))^2\mid X]- (\bar J(X)-\bar J(X) )^2 \right] + var( \bar J(X) ) \\ &= \mathbb E_X\left[ \mathbb E_Y[(J(X,Y)-\bar J(X))^2\mid X] \right] + var( \bar J(X) ) \\ &= \mathbb E_{X,Y}\left[ (J(X,Y)-\bar J(X))^2 \right] + var( \bar J(X) ) \\ \end{align} $

i.e.:

$ var(J(X,Y)) \geq var( \bar J(X) ) $

Estimation from MC:

  • crude MC sampling of$ X, Y $ pairs:$ \hat J \approx \bar J = \mathbb E_{X,Y} [J(X,Y)] $
  • rao-blackwellized MC sampling: We need only the$ X $ values:$ \tilde J \approx \bar J = \mathbb E_{X} [\bar J(X)] $

Exercise

Assume we draw samples from a multivariate Gaussian. Here we make things simple and assume that the covariance matrix$ \Sigma $ is diagonal:

$ \begin{pmatrix} x \\ y \end{pmatrix} \sim \mathcal N \left(\vec \mu, \Sigma \right) $

with $ \vec \mu = \begin{pmatrix} 1 \\ -2 \end{pmatrix} $

$ \Sigma = \begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix} $

We want to estimate the expectation$ \mathbb E_{X,Y} \left[J(X,Y)\right] $ with $ J(X,Y) = 3x + 2y + 5xy $

What is$ \bar J(X) $?

Sample from the 

mu_x = 1.
mu_y =-2.
mu = np.array([mu_x, mu_y])
def sample(size=20, 
    mu = mu, 
    sigma=np.array([[2., 0.], [0., 3.]])): 
    xy = np.random.multivariate_normal(mu, sigma, size=size)
    x = xy[:,0]
    y = xy[:,1]
    return x,y
x,y = sample(size=1000)
plt.xlabel("x")
plt.ylabel("y")
plt.plot(x, y, "b.");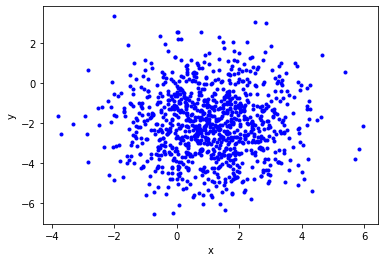
cell-output
def f_xy(x,y):
    return 3*x + 2*y + 5.* x*y
plt.title("MC estimation histogram (sample size:"+str(size)+")")
plt.hist(cmcs, density=True, alpha=0.5, bins=30,label="crude MC")
plt.hist(rbmcs, density=True, alpha=0.5, bins=20, label="Rao-Blackwellized MC")
plt.axvline(true_expectation, color ="k", label="true expectation")
plt.legend();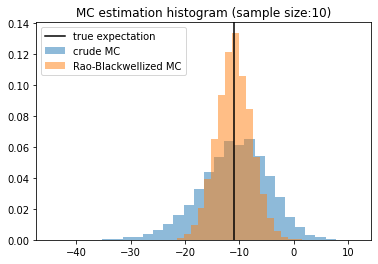
cell-output
print("variance of crude estimator", cmcs.var(ddof=1))
print("variance of rao-blackwellized estimator", rbmcs.var(ddof=1))
print(cmcs.var(ddof=1)," approx ", rbmcs.var(ddof=1) + ((cmcs-rbmcs)**2).mean() )
variance of crude estimator 39.59392224154448
variance of rao-blackwellized estimator 10.050073774591121
39.59392224154448  approx  39.21136575157144

Literature: